Sistem Bilangan Komputer
Number system, Format bilangan komputer atau sistem bilangan komputer merupakan sebuah cara untuk mewakili besaran yang berasal dari sebuah item fisik. System bilangan memakai sebuah bilangan basis atau base otr radix atau dikenal dengan bilangan dasar yang menjadi tertentu. Dalam kaitan nya dengan komputer, terdapat 4 jenis system bilangan yang di ketahui yakni : decimal (basis 10), biner (basis 2), octal (basis 8), dan juga hexadecimal (basis 16).
Berikut Penjelasan macam-macam Sistem Bilangan Komputer :
- Biner
Biner atau basis 2 merupakan system bilang yang terbagi daei 2 simbol yakni 0 dan juga 1. Bilangan biner atau basis 2 ini di kenal kan dan di populerkan oleh john von Neumann. Dan untuk system bilangan modern itu di cetus kan oleh Gottfried Wilhelm Leibniz di abad ke 17. Pada sistem bilangan komputer basis 2 atau binner ini merupakan suatu dasar dari seluruh system bilangan berbasis digital. Di system binner, anda bisa mengkonversi nya ke pada system bilangan hexadecimal atau octal. Pada system ini juga bisa di sebut dengan istilah binary digit atau bit.
- Octal
Octal atau basis 8 merupakan sistem bilangan komputer yang terbagi dari 8 simbol yakni 0, 1, 2, 3, 4, 5, 6, dan juga 7.
- Hexadecimal
Hexadicemial atau basis 16, hexa yang artinya 6 dan decimal yang artinya 10 merupakan suatu system bilangan yang terbagi dari 16 simbol yakni 0, 1, 2 , 3, 4, 5, 6, 7, 8, 9, A(10), B (11), C (12), D (13), E (14), F (15). Di dalam sistem bilangan komputer hexadesimal ini mengkombinasi kan 2 unsur yakni huruf dan juga angka. Untuk huruf A itu yang mewakili angka 10, huruf B itu yang mewakili angka 11, dan juga seterusnya hingga pada akhir nya sampai pada huruf F yang mewakili angka 15.
- Decimal
Berarti persepuluhan atau bilangan berbasis 10. Biasanya Bilangan tersebut adalah 0 sampai dengan 9. Bilangan ini merupakan bilangan yang sering digunakan secara umum oleh manusia untuk perhitungan matematika. Contoh penulisan (23)10.
Tabel Konversi Sistem Bilangan
KONVERSI BILANGAN
1. Biner
A. Biner ke Desimal
Konversi Biner ke Desimal dikerjakan dengan cara 2^n mulai dari biner sebelah kanan hingga kiri dengan kelipatan n.
Bilangan Biner 1011010 adalah 90 dalam bilangan Desimal
Cara Pengerjaan :
1 0 1 1 0 1 0
64 32 16 8 4 2 1
Yang bernilai 1 (digarisbawahi) dijumlahkan
64 + 16 + 8 + 2 = 90
B. Biner ke Desimal
C. Biner ke Hexadecimal
2. Desimal
A. Desimal ke Biner
B. Desimal ke Oktal
C. Desimal ke Hexadecimal
3. Oktal
A. Oktal ke Biner
B. Oktal ke Desimal
C. Oktal ke Hexadecimal
4. Hexadecimal
1. Hexadecimal ke Biner
2. Hexadecimal ke Desimal
3. Hexadecimal ke Oktal
Mencari ke Biner, di jawaban sebelumnya sudah ditemukan Biner dari 54 adalah 1010100.
Maka tinggal dicari oktalnya dengan membuat pemisah setiap 3 bilangan selanjutnya.
Operasi Aritmatika pada Sistem Bilangan Komputer (Tanpa dikonversi)
1. Bilangan Biner
Penjumlahan
Dalam bilangan biner terdapat dua aturan dasar,
antara lain:
0 + 0 = 0
1 + 0 = 1
0 + 1 = 1
1 + 1 = 1, simpan 1
Sebagai cara penjumlahan bilangan desimal yang kalian kenal sehari-hari, penjumlahan bilangan biner juga harus selalu memperhatikan carry (sisa) dari hasil penjumlahan pada tempat yang lebih rendah.
Contoh :

Pengurangan
Cara Pengurangan :
0 - 0 = 0
0 - 1 = 1 borrow 1 (jika masih ada angka di sebelah kiri)
1 - 0 = 1
1 - 1 = 0

Perkalian
1. Pada perkalian biner pada dasarnya sama dengan perkalian desimal,bedanya hanya nilai yang dihasilkan hanya 0 dan 1.
2. Bergeser 1 ke kanan setiap dikalikan 1 bit pengali
3. Setelah proses perkalian masing-masing bit pengali selesai, lakukan penjumlahan masing-masing kolom bit hasil.

Pembagian
1. Pembagian biner pada dasarnya sama dengan pembagian desimal, bedanya nilai yang dihasilkan hanya 0 dan 1
2. Bit-bit yang dibagi diambil bit per bit dari sebelah kiri. Apabila nilainya lebih dari bit pembagi, maka bagilah bit-bit tersebut. Jika setelah bergeser 1 bit nilainya masih dibawah bit pembagi, maka hasil bagi sama dengan 0.

2. Bilangan Oktal
Penjumlahan
Berikut adalah tahapan untuk operasi penjumlahan oktal, antara lain:1. tambahkan masing-masing kolom secara desimal
2. rubah dari hasil desimal ke dalam bilangan oktal
3. tuliskan hasil dari digit paling kanan dari hasil oktal
4. jika hasil penjumlahan pada masing-masing kolom terdiri dari dua digit, maka digit paling kiri adalah carry of untuk penjumlahan kolom berikutnya.
5. sisa akan muncul atau terjadi apabila jumlahnya sudah melebihi 7 pada setiap tempat.

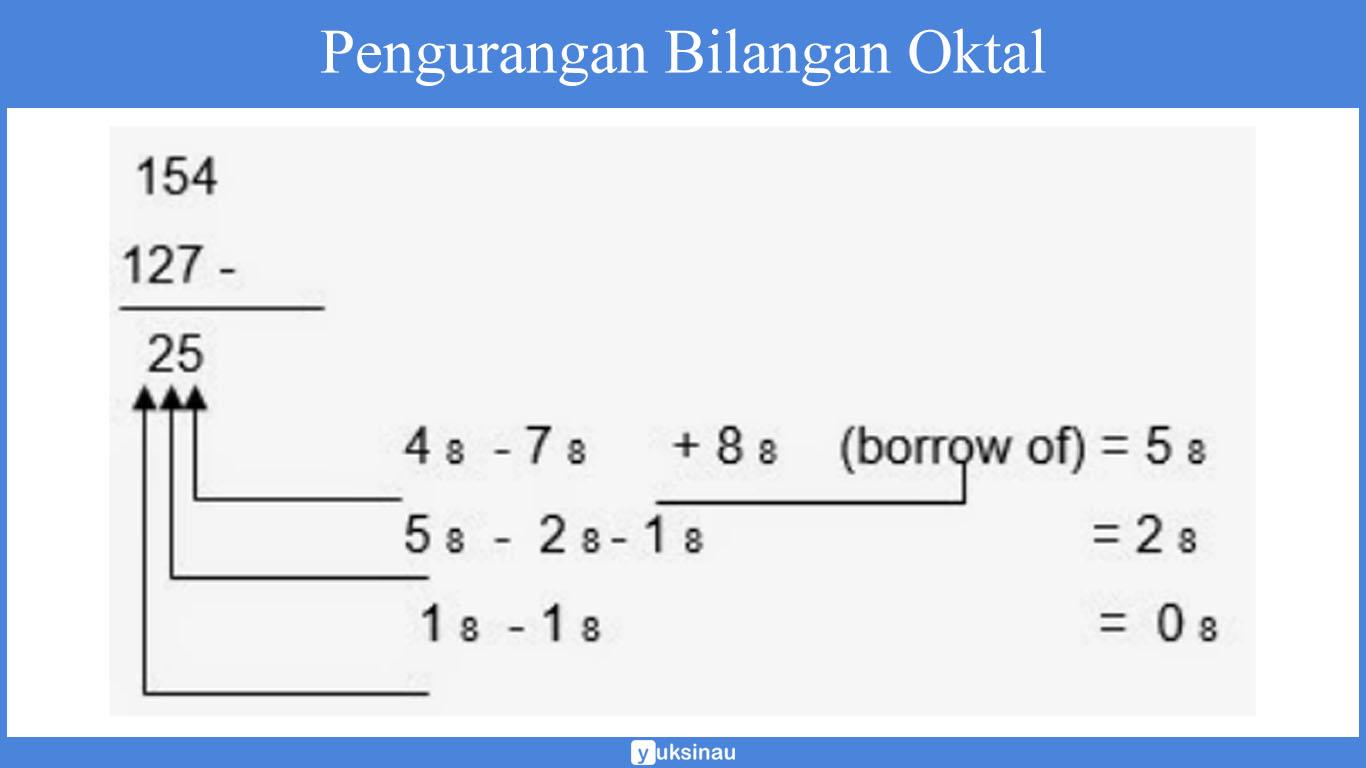
Pengurangan
Pengurangan Oktal bisa dilakukan dengan cara yang sama dengan yang ada pada operasi pengurangan bilangan desimal.Pada pengurangan apabila bilangan yang dikurangi lebih kecil dari pada bilangan pengurangnya maka akan dilakukan peminjaman (borrow) pada tempat yang lebih tinggi (dengan nilai 8).
Perkalian
Berikut adalah tahapan untuk operasi perkalian oktal, antara lain:1. kalikan masing-masing kolom secara desimal.
2. rubah dari hasil desimal ke bilagan oktal.
3. tuliskan hasil dari digit paling kanan dari hasil oktal.
4. jika hasil perkalian pada masing-masing kolom terdiri atas 2 digit, maka digit paling kiri adalah carry of untuk ditambahkan pada hasil perkalian pada kolom berikutnya.

Pembagian

Hexadecimal
Penjumlahan
Dalam penjumlahan bilangan heksadesimal, sisa akan terjadi atau berlangsung apabila jumlah dari masing-masing tempat melebihi 15.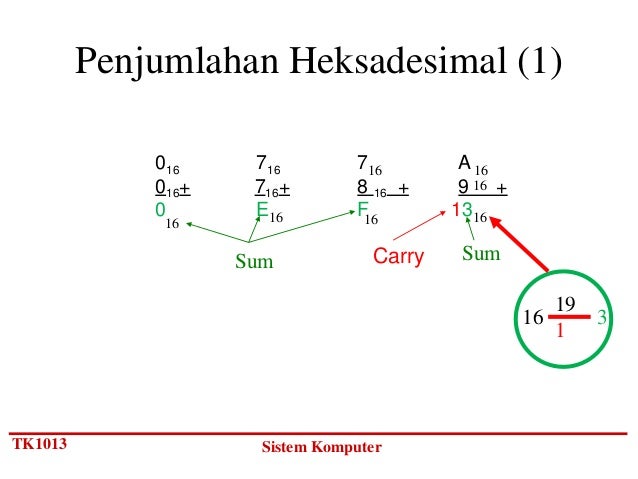
Pengurangan

Perkalian

Pembagian

Daftar Pustaka :















Komentar
Posting Komentar